Playing magic tricks with randomness

Us programmers are a very fussy bunch. On the one hand, we want the ability to generate random numbers at a whim with all the properties we expect of a truly random generator. On the other hand, we want (neigh, expect) our programs to be re-producible, deterministic and testable. Fortunately, we’re also a crafty a bunch, so we’ve managed to solve this conundrum to a pretty satisfying degree of accuracy. How did we do it?

We have to start off by clearing up what exactly the goal is when we say we want a “random number generator.” In reality, what we want is some generator, $f$ such that for some seed $x_0$ the resulting sequence of numbers $\{f(x_0), f^2(x_0), \ldots, f^n(x_0)\}$ look independent and identically distributed. What does that mean? Well, the independent part is self-explanatory, but being identically distributed simply means that our sequence of random numbers come from the same distribution. So if the first number in the sequence is supposed to have a uniform distribution over the interval $[0,1]$ then so should the second, third and every other number in the sequence too.

In case the syntax is confusing, recall that $f^2 = f\circ f$, $f^3 = f\circ f\circ f$ and so on…

Okay, I’m no mathematician (okay I totally am) but that sequence of numbers definitely does not look independent. In fact, they’re not just dependent on each other, they’re completely determined by the same exact two pieces of information! If I know the generator usd and the seed I can predict, with 100% accuracy, the $i^{th}$ “random” number in the sequence. Ah, but that’s the point, see? We wanted determinism, so the price to pay is not having true randomness.

In statistics literature it is the norm to see the phrase “independent and identically distributed” abbreviated as IID

So we’ve cleared up what we want: a generator that can fool anybody into thinking it produces random numbers when in reality it doesn’t. Simple, right? So, umm… got any ideas on what that generator might look like?

Preliminaries

Most everyone knows that computers store data as binary strings, but something less often discussed is the math behind these binary values. The field falls under the branch of Galois theory. We won’t delve too deep here; I just want to introduce one concept called the finite field. Specifically we’re going to define the Galois field $\mathbf{F}_2$.

A field in math is a set of elements that have been endowed two binary operators (addition and multiplication) and follow the field axioms. Most fields we’ve worked with in high school are infinite - the set of real numbers $\mathbf{R}$, the set of integers $\mathbf{Z}$, etc… Finite fields, on the other hand, are fields with (you guessed it) a finite number of elements. The most important of these finite fields are called Galois fields and they’re constructed as the set of integers modulo a prime number, $\mathbf{F}_p$.

Another notation people use for Galois fields are $\mathbf{Z}/p\mathbf{Z}$ for some prime number $p$

Let’s get a little less abstract and start talking about the specific Galois field when $p=2$. The field $\mathbf{F}_2$ contains two elements: 0 and 1. Since there’s only two tables we can define addition and subtraction by listing all the possible combinations:

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 0 = 1
• 1 + 1 = 0

Woah! What’s up with that last one? No, that’s not a typo; we had to define addition in an odd way because we’re dealing with a finite field, and one of the necessary properties of a field is that adding two elements from the field has to give back another element of the field. In other words, we can’t define addition as $1+1=2$ because $2$ is not an element of the field $\mathbf{F}_2$.

Multiplication is not as flashy as addition and we can define it in the familiar way:

• 0 * 0 = 0
• 0 * 1 = 0
• 1 * 0 = 0
• 1 * 1 = 1

If you look at these rules for addition and multiplication you might notice they map perfectly to logical XOR and logical AND respectively. This is great news for us because computing XOR and AND is extremely efficient in computer code, since the CPU contains many instances of these logic gates in physical hardware.

Onto the good stuff

So we now know that addition in $\mathbf{F}_2$ is achieved through XOR, but how do we use that to generate new numbers?

First Attempt: Shift-Register Generators

Here’s one idea: we have the seed value, $x_0$, but we still need to generate a new number from it. So let’s make use of the bit shift operator to get some new, intermediate number that we will use like so: $x_{i+1} = x_i \oplus (x_i \gg u)$ where we pick some $u$. For various math reasons¹ we actually can’t pick the shift(s) willy nilly but instead we have to pick pre-determined correct combinations of shift. One such combination that works well for 32-bit computer words is $(13,17,5)$ which can be implemented like so:

uint32_t xorshift32(uint32_t a) {
	uint32_t x = a ^ (a << 13);
	x ^= x >> 17;
	x ^= x << 5;
	return x;
}

This method of generating random numbers is extremely fast, but it only has a period of $2^{32}-1$ (meaning you can only call it $2^{32}-1$ times before the sequence starts repeating itself). This, combined with the fact that it’s fully linear (remember that XOR is just addition and bit shifts can be represented as matrix multiplication) makes it not pass all the sniff tests people have come up with over the years. It’s also definitely not cryptographically secure and should not be used for generating secrets.

A better attempt: Mersenne Twister

Fully explaining the Mersenne Twister would be quite beyond the scope of a blog post, but we can definitely take a look at the core differences between the two (and implement it!)

First thing we need to define are the parameters of the Mersenne Twister. The most important values are:

• w: word size (in number of bits)
• n: degree of recurrence
• u, d, s, b, t, c and l: More coefficients involved with generating the next number in the sequence

The full list of coefficients are here:

template <typename num_t> struct MTcoefs {
  num_t w, n, m, r, a, u, d, s, b, t, c, l, f;
};

One of they key differences with the MT algorithm is that we now will store additional state. The main purpose of this state is to increase the period of the sequence. We will want an array of length n where each element is a computer word of length w. We also need an index to tell us where in the array we’re at. We can store this state as a new data type:

constexpr auto LWBO(auto w, auto s) {
  return ((1L << w) - 1) & s;
}

template <typename num_t, MTcoefs<num_t> coefs>
struct MTGen {
  std::array<num_t, coefs.n> gen;
  size_t index;
  const num_t lower_mask = (1L << coefs.r) - 1;
  const num_t upper_mask = LWBO(coefs.w, ~lower_mask);
};

To initialize the state, we need to set the index to $n$ (not 0) and use the following formula:

the constructor method of the state hence can be written like so:

auto seed_reccurance(auto x_prev, auto i) {
  return coefs.f * (
    x_prev ^ (x_prev >> (coefs.w - 2))) + i);
}

MTGen(num_t seed) {
  index = coefs.n;
  gen[0] = seed;
  for (size_t i = 0; i < gen.size(); i++) {
    auto in_ = seed_reccurance(gen[i-1], i);
    gen[i] = LWBO(coefs.w, in_);
  }
}

Once the setup is taken care of, generating a new number in the sequence is actually quite similar to the previous attempt. The main difference is that now we also are using bitwise AND which, if you recall, corresponds to multiplication in the field $\mathbf{F}_2$:

auto extract_number() {
  if (index >= coefs.n) twist();
  auto y = gen[index];
  y ^= (y >> coefs.u) & coefs.d;
  y ^= (y << coefs.s) & coefs.b;
  y ^= (y << coefs.t) & coefs.c;
  y ^= (y >> coefs.l);
  index++;
  return LWBO(coefs.w, y);
}

Once we blast through the entire array we need to do something called “twisting” which you can kind of think of as randomizing the old state into some new state. We also reset the index back to 0:

void twist() {
  for (size_t i = 0; i < gen.size(); i++) {
    auto x1 = (gen[(i + 1) % coefs.n] & lower_mask);
    auto x2 = (gen[i] & upper_mask);
    auto x = x1 | x2;
    auto xA = (x >> 1);
    if ((x % 2) != 0) xA ^= coefs.a;
    gen[i] = gen[(i + coefs.m) % coefs.n] ^ xA;
  }
  index = 0;
}

Finally we can run this program by defining the coefficients of the algorithm and generating new numbers in a for loop:

int main() {
  using num_t = uint32_t;
  constexpr MTcoefs<num_t> mt_32{.w = 32,
                                 .n = 624,
                                 .m = 397,
                                 .r = 31,
                                 .a = 0x9908b0df,
                                 .u = 11,
                                 .d = 0xFFFFFFFF,
                                 .s = 7,
                                 .b = 0x9D2C5680,
                                 .t = 15,
                                 .c = 0xEFC60000,
                                 .l = 18,
                                 .f = 1812433253};
  num_t seed = 0;
  size_t num_generate = 0;
  MTGen<num_t, mt_32> generator{seed};
  std::ofstream file_handle{"sample.dat"};
  for (size_t i = 0; i < num_generate; i++) {
    file_handle << generator.extract_number();
    file_handle << std::endl;
  }
}

Results

Recall that all the generators we discussed are meant to produce a sequence of random variables that are normally distributed, so we actually have to check just how normally distributed these numbers were! Let’s attempt 3 versions: generating a small initial sequence, generating a moderately sized sequence and generating a really long sequence:

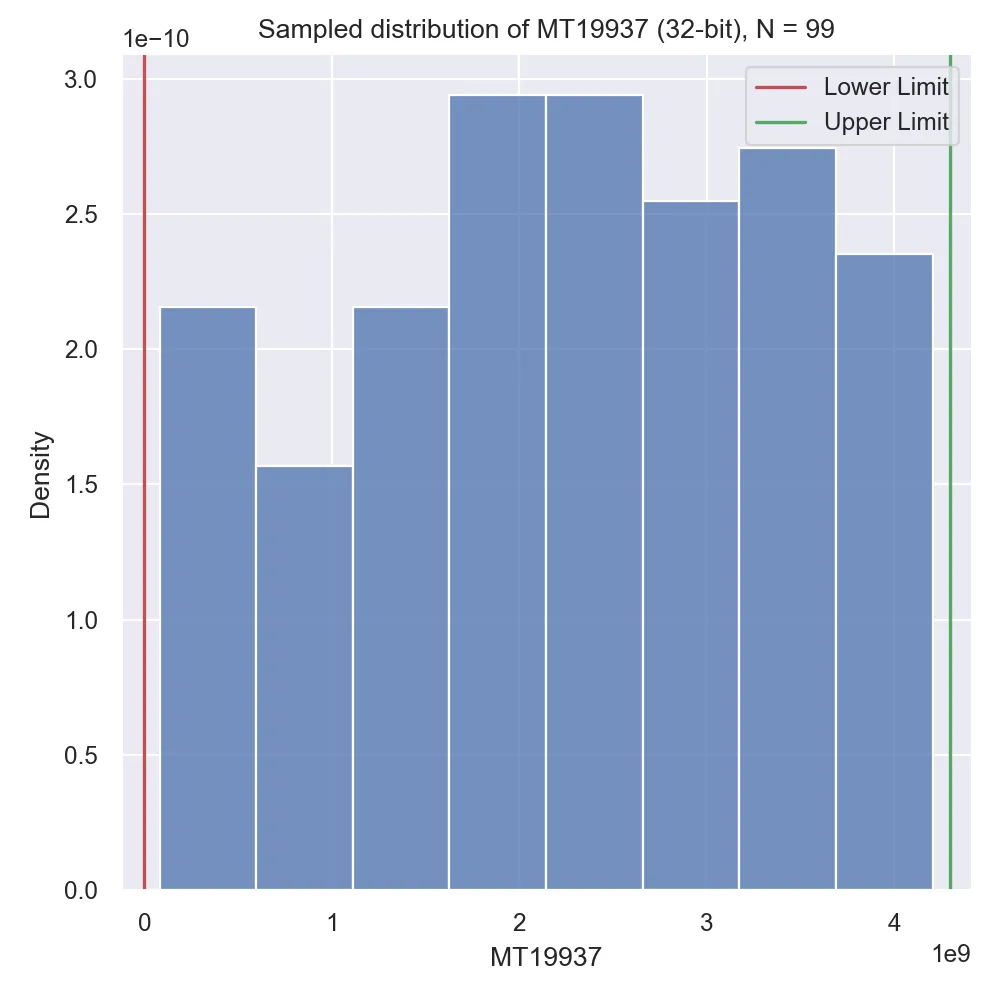
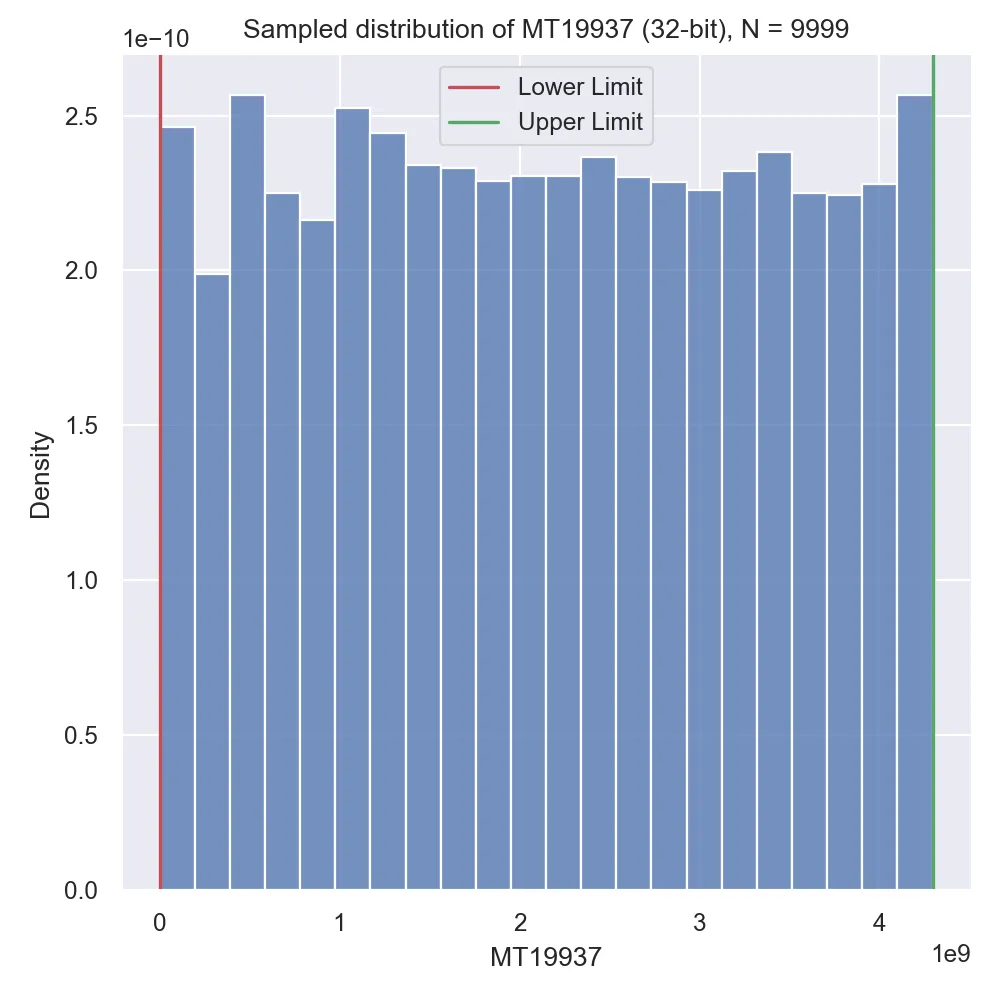
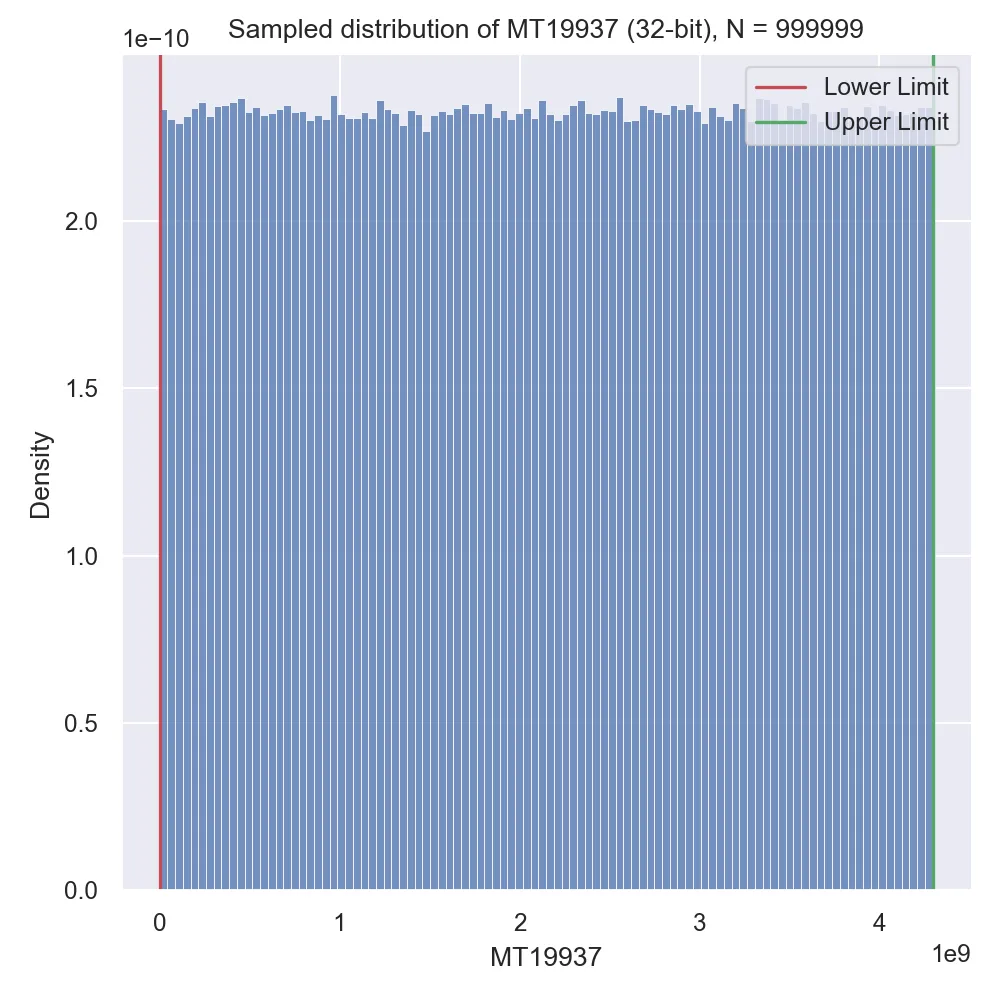
Looking at the results we can see an effect called “burn-in,” which is basically when a random number generator has poor statistical properties for the first section of its sequence but progressively gets better statistical properties the further out into the sequence we get. MT19937 is surely known for this disadvantage (at least, compared to other modern generators).

Conclusion

We learned what the goal of random number generators are, some of the theory behind the popular generators and looked at results. Overall, mathematicians have made huge leaps and strides on a problem that seems contradictory at face value: make a machine specifically engineered to be deterministic operate with a perceived randomness. But we made it work, and not only that but the codegen also maps extremely efficiently to hardware! And they said we couldn’t have our cake and eat it too.